Augmenting Learned Centroidal Controller with Adaptive Force Control
Quadruped Locomotion
Reinforcement Learning
L1 Adaptive Control
Robustness
Research Objective
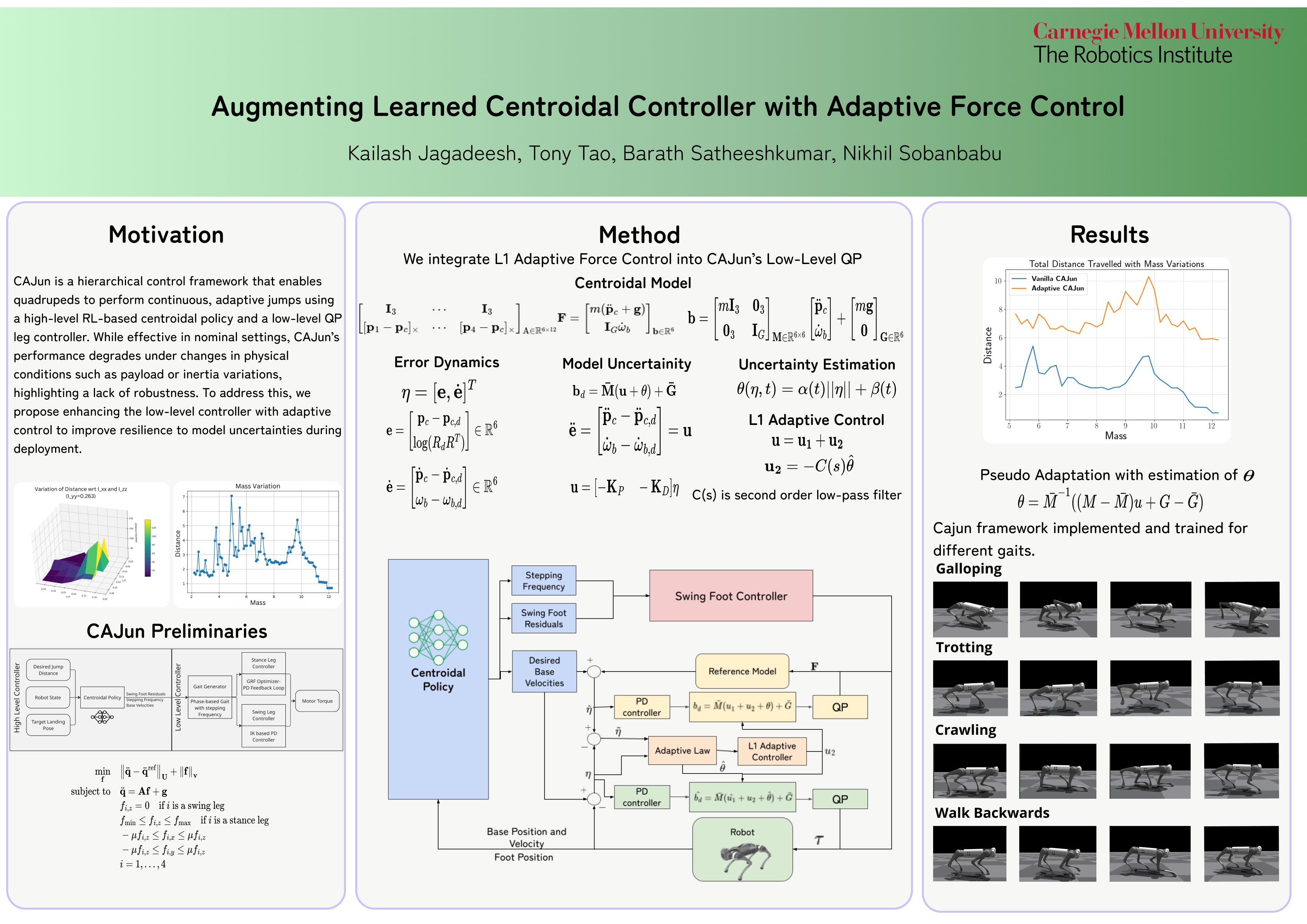
This work enhances the CAJUN hierarchical reinforcement learning framework for quadrupedal jumping by introducing an L1 adaptive control augmentation to the low-level Quadratic Program (QP) solver. While CAJUN excels at learning centroidal motion policies for continuous jumping, it suffers from degraded performance under dynamic changes and sim-to-sim transfer. Our goal was to improve robustness to model uncertainty and payload variation by integrating adaptive force compensation directly into the control loop.
Key Features Achieved
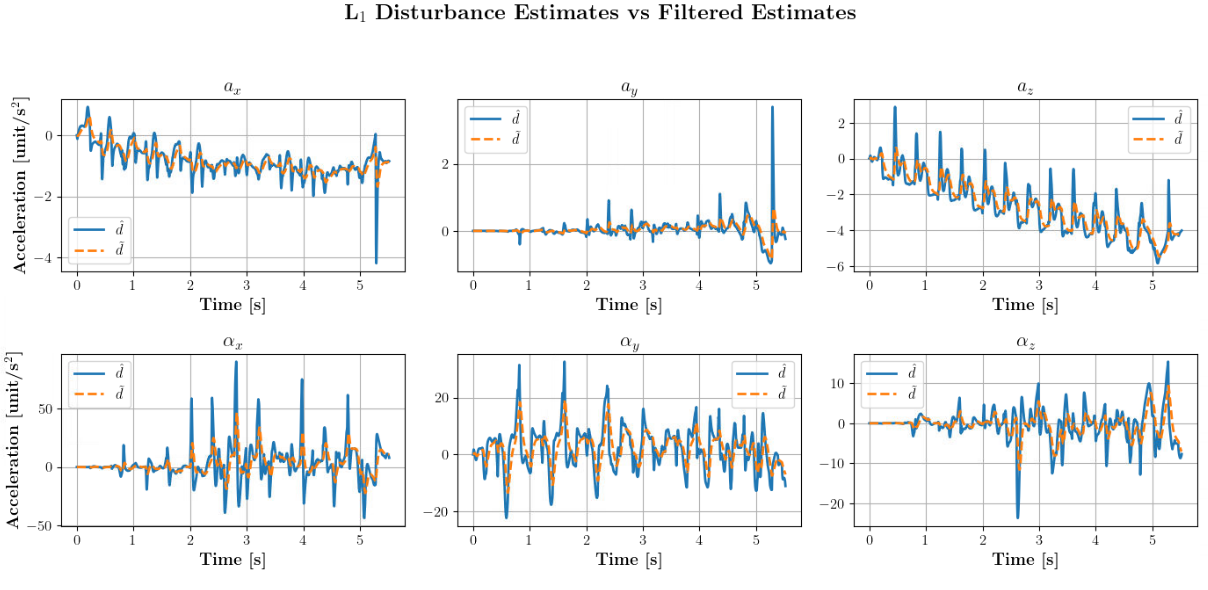
- Implemented L1 adaptive law to estimate and compensate unmodeled disturbances in centroidal wrench space.
- Modified CAJUN’s low-level QP solver to include filtered disturbance feedback for real-time adaptation.
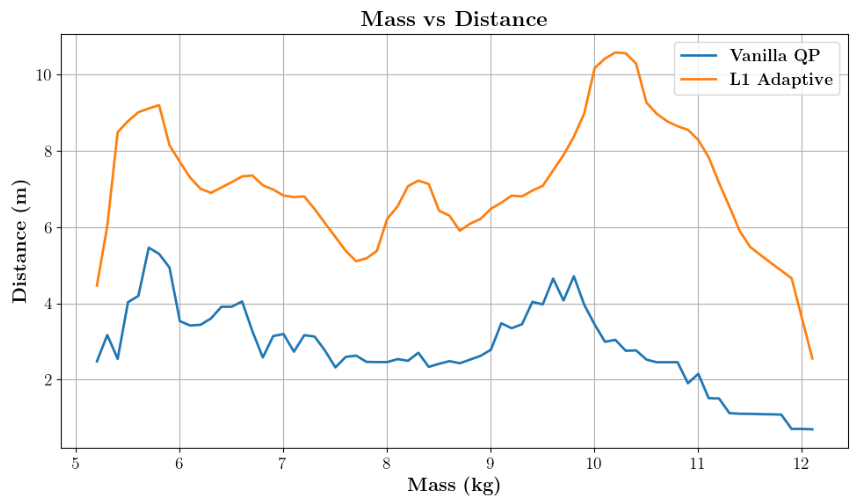
- Validated robustness under varying payloads (up to 2× nominal mass) and inertia mismatch in MuJoCo simulations.
- Demonstrated consistent jump trajectories and ~4× performance gain over baseline QP controllers in perturbed setups.
- Achieved stable low-frequency adaptation with high-frequency control loops through discrete low-pass filtering.
Challenges & Learnings
- Observed CAJUN’s sensitivity to simulator-specific inertial parameters, requiring careful dynamic calibration.
- Addressed instability in disturbance feedback by tuning cutoff frequencies of the L1 filter for smooth adaptation.
- Gained deeper insight into centroidal dynamics modeling and the trade-off between fast adaptation and stability margins.
- Learned integration of model-free learning with adaptive model-based control for hybrid locomotion frameworks.